We’ve already come across the words Stellation and Stellated when we looked at The 4 Star (Kepler-Poinsot) Polyhedra, and we made frequent use of stars in The 53 Semi-Regular Non-Convex Polyhedra – but it’s useful here to have a proper look at Stellation. It’s all about creating stars, or star points, by extending the edges of the usual convex polygons, and a flat heptagon (7-sided) shows this rather well.
First we take the heptagon and extend its sides out as far as we can. Then we look where the extended lines cross first: this is the First Stellation (7-2). If they cross again this gives us a Second Stellation (7-3).
With a heptagon we get two Stellations: they are referred to as 7-2 and 7-3 as a way of distinguishing the number of points round the shape that the grey lines cross. Beyond this there are no others: by now the grey lines are all diverging from each other and none of them will ever meet again.
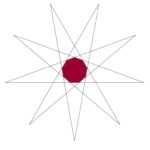
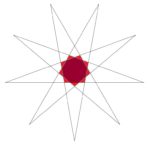
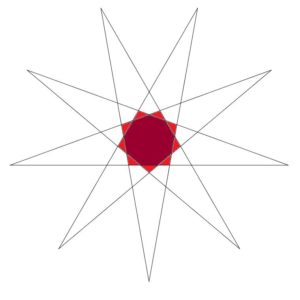
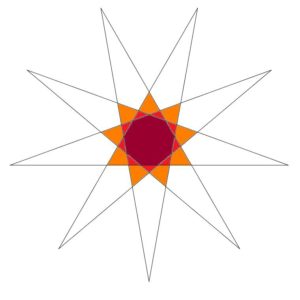
The pentagon we already looked at gave us only one stellation – the 5-pointed star – but for higher numbers of sides we get more. Here are the stellations of the enneagon (9 sides):
The final stellation always has the sharpest points, and they usually extend a long way beyond the original polygon.
So now we understand how to stellate a polygon, let’s crack on and see how to stellate polyhedra in Stellations of the Dodecahedron.