When we looked at the 5 Platonic and 13 Archimedean Solids we seemed to cover all possible combinations of polygons at each vertex – we even said the sets of Platonics and Archimedeans were full. But there’s a curious extra set of the convex Archimedean Solids, namely Prisms and Antiprisms. This is actually an infinite set, so it’s quite something to have left them out!
Say Prism and people think of a triangular cross-sectioned piece of glass which splits white light into its component parts. They don’t consider that the sides of the prism are actually squares: neither do they realise that we define a general prism as two regular polygons of any number of sides sandwiched together with a strip of squares. If this seems hard to get your head round, the following may help:
By this definition prisms can be triangular, hexagonal, heptagonal, or anything you like – icosikaigonal (which I think is 23-sided) might be quite fun. Even a cube is just a special case: we could call it a square prism if we chose to.
Clearly the set of possible prisms goes on for ever, since there’s no limit to the number of edges the two polygons can have. And each prism meets the criteria of the Archimedean Solids – namely that they have the same mix of regular polygons round each vertex. But they’re not usually considered with the other Archimedeans, probably because they’re not so rotationally symmetric, they’re not so beautiful, and they’re actually rather boring: once you’ve understood one you’ve basically understood the whole lot right out to infinity.
Once we’ve dealt with square sides, we can pick up an idea we looked at when we discovered snub polyhedra earlier on. Sometimes where you have squares doing a sort of joining things together job, you can replace them with pairs of triangles in a rhombus, or diamond, formation. This usually also requires twisting the rest of the shape a bit, and sometimes you can get away with it: and it turns out you always can do this for prisms. By rotating one of the n-gons to totally mis-align the points this leads us to Antiprisms. Again there’s an infinite set of these, and they look rather like the stringing on traditional drums…
Now I’ll mention the word ‘non-convex’, which takes us to star polygons and their associated prisms. In our previous work we were limited to 5, 8 and 10-pointed stars, but in the world of prisms new possibilities open up. All that’s needed is to be able to make a star out of the points, so we can also go for 7, 9, 11 or in fact any number where we can draw a real star between the points. (This still rules out 6, where the usual “Star of David” is actually just two triangles – but even that shape is interesting in its way: it turns out to be a compound of two octahedra, each of which is a triangular antiprism in its own right. We’ll give this one a special mention down below…)
Intriguingly for a number like 7 we can draw two different stars – so there are two different forms of the star prism! We note them as 7-2 and 7-3:
For most higher values of n there are many different stars of the form n-p, though for 8, 10 and 12 there’s only one. The precise maths to explain this isn’t very difficult, but I won’t go into it here other than listing them below:
|
n |
Possible n-grams (star polygons) |
| 2 | none |
| 3 | none |
| 4 | none |
| 5 | 5-2 |
| 6 | none, though people often think the Star of David is valid |
| 7 | 7-2, 7-3 |
| 8 | 8-3 (the familiar octagram) |
| 9 | 9-2, 9-4 |
| 10 | 10-3 (the familiar decagram) |
| 11 | 11-2, 11-3, 11-4, 11-5 |
| 12 | 12-5 |
There are, of course, a corresponding set of antiprisms. These get very complex, and very beautiful…
One might think this was the end of the story, but rather like with the non-convex semi-regular polyhedra we can also postulate forms where we let the squares or triangles slice back under the n-gons or the n-grams, running right through the centre of the shape and creating a sort of re-entrant undercut “crossed” version. This doesn’t actually work for convex (polygonal) prism or antiprism forms: the squares and triangles just won’t stretch far enough across to their opposite counterparts. Neither does it work for squares in starred (polygrammic) prisms, because the edges just don’t go in the right directions.
For triangles in starred antiprism forms, however, it does work – though even then only for stars of the form n-p where p is (strictly) between n/3 and n/2. (I worked this out as I sat in church one morning.) So the 5-2 and 7-3 stars work, but the 7-2 star doesn’t. For 9 sides only the 9-4 works (9-3 is not really a valid shape anyway – it’s another one like the Star of David) and once we get to 11 we find that both the 11-4 and 11-5 stars work. Beyond 11 I believe there are always plenty of forms which work.
This last point – that for an 11-sided prism we can find more than one crossed re-entrant undercut antiprism form – seems to me to be the last interesting thing we can say as n increases – hence my comment earlier that there’s nothing interesting in the world of prisms beyond 11!
I’ve hardly seen any of these ‘crossed’ forms drawn up even as diagrams, and certainly no-one seems to have done any serious analysis or photographed any models – so perhaps there’s another PhD out there to be got. But I did find this one diagram of a crossed penatgrammic antiprism. Interestingly although ‘anti’ would normally suggest the two star faces are twisted out of alignment with each other, because the triangles cut back through the shape the stars come back into alignment here (not really sure the picture confirms this, though.) So you could, if you were so minded, derive this one by carving it out of an ordinary pentagrammic prism.
Some day I’ll build one of these for myself, but it ain’t gonna be soon.
Lastly in this section, here are George Hart’s two beautiful shots of a 25-12 Crossed Antiprism taken from George Hart’s page on Virtual Polyhedra. Needless to say they’re only virtual renderings – no-one has actually built one of these things – but what a cracker it is:
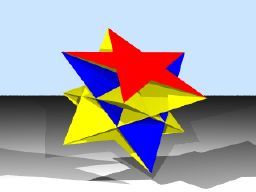
Meanwhile although I don’t usually do group shots, I reckon my collection of Heptagonal and Heptagrammic Prisms and Antiprisms looks so pretty that I’m going to show a couple here. In time, of course, it’ll also include the “crossed” one.
Before we leave the Prism family, let’s just have a last look at one I ruled out earlier – which I’ll now call a “False Hexagrammic Antiprism”. Although you can draw a good star on 5 points (the usual pentagram) you simply can’t do it on 6: the best you can do is two overlapping triangles, the familiar Star of David. This shape has no relevance at all as a “star” in polyhedral modelling, though we noted a very curious ‘near thing’ at W110 under The Non-Convex Semi-Regular Polyhedra.
Despite the “falseness” of the Star of David in this context, it hasn’t stopped people building things which certainly look like prisms and antiprisms. In reality they’re better described as “compounds” based on the two triangles in the star: the prism form is a compound of two triangular prisms, while the antiprism form is a compound of two triangular antiprisms (which happen also to be octahedra.) But this “falseness” doesn’t make the finished shapes any less attractive. G. Korthal Altes offers a huge range of nets without mentioning that this one’s “false”, and amazingly my friend Valerie took up the challenge after a long discussion of antiprisms in the margins of the Cheltenham Literature Festival. Here is Altes’ model…
That’s just about all there is to say about Prisms and Antiprisms, or indeed about all of the Uniform Polyhedra (i.e. those where all the vertices are the same.) But if you’ve tried making any of these you’ll know there are all kinds of ways you can ‘get it wrong’. This is the subject of our next topic, The 92 Johnson Solids.