The duals of the 13 Archimedean Polyhedra are called the Catalan Polyhedra, and these turn out to be rather pleasing variations on what we’re already familiar with. As we’ve said elsewhere, the point is to match vertices with faces and faces with vertices.
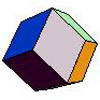
An oddity of the duals is that since all the faces are the same there’s no strong reason to give them different colours. As a result these models aren’t quite so immediately eye-catching – their beauty is mainly in the structures of their edges and the way they connect the vertices. To demonstrate that point – if you look at the Truncated Cube below on the left, you’ll see its faces are triangles and octagons; so it’s dual model on the right, the Triakis Octahedron, should have 3-edge vertices and 8-edge vertices. As indeed it does!
Here is the complete table of Archimedan Solids and their counterparts the Catalan Solids:
Following the course of the Polyhedra our next question should be concerning the 4 Star (Kepler-Poinsot) Polyhedra: but as we saw in Compounds these are actually duals of each other. So our next move is to Duals of the 53 Semi-Regular Non-Convex Polyhedra.