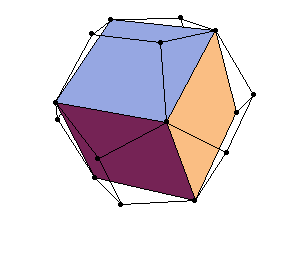
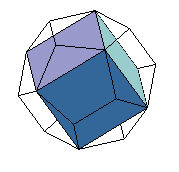
We’re already seen that we can fit 2 Tetrahedra inside a cube, to get the Stella Octangula or Compound of Two Tetrahedra:
It turns out we can also fit a cube inside a dodecahedron; and we can do it five different ways.
Here is a model showing the 5 cubes:
As you look in detail at these models you can make out the coloured cubes quite easily – particularly the red one and the blue one. If you then focus on the detail you start to see all sorts of curious other shapes forming – stars, dimples, triangles and so on. You notice the skeletons of some of the non-convex semi-regular polyhedra…and then you can just stand back and enjoy the whole big thing again. If you sense it has an overall dodecahedral shape, well – yes it does – after all, this is the model of 5 cubes in a dodecahedron!
It doesn’t stop there. If you consider each cube contains two tetrahedra, we can pick sets of either 5 or 10 tetrahedra and build the models of the compounds. Here is a model of 5 tetrahedra in a dodecahedron:
A stick model of the Compound of 5 Tetrahedra is a favorite test of strength among people who do Modular Origami. I’ve never yet made it without everything collapsing in a heap, but some people make a really nice job of it. It may be that the quality of the paper helps…or perhaps it’s spit, or even (heaven forbid) glue:
Obviously there’s a twist to this compound – i.e. left or right – and you could make a mirror image of it with the other twist (the technical name is enantiomorph.) Putting the two together makes a Compound of 10 Tetrahedra. I’ve never managed to construct this in a way which makes the colours convincing – it’s actually not possible – so I find little reason to actually make it: but here is a picture of one I found on the internet:
Next we can observe that the dual of a cube is an octahedron, and the dual of a dodecahedron is an icosahedron – so as well as inscribing cubes in a docecahedron we should be able to circumscribe octahedra around an icosahedron. Here indeed is the Compound of 5 Octahedra around an Icosahedron:
This exhausts the main mathematical interest in compounds, but a curious one is certainly the Compound of 5 Dodecahedra. This one doesn’t have much use mathematically, but it’s quite pleasant to look at: I made a model once but it was enormous (those are my arms in the photo) and I’m afraid it hasn’t survived.
Other than this, there are a number of Compounds that are just pretty to look at. Follow the link to Compounds of Cubes and Octahedra .