We’re back in the land of the Archimedean Duals, the Catalan Solids, here. Stellating one of them, the Rhombic Dodecahedron, was quite easy, since its geometry was fairly simple and in the end it only had three or four real stellations. The other Catalan solids pose bigger challenges, because even at the start they have large numbers of oddly-shaped faces intersecting at some really strange angles. Just working out the basic geometry here is quite difficult, let alone analysing the myriad three-dimensional ‘cells’ that make up the stellations. But the results are well worth the effort: some of these are the most beautiful polyhedra I’ve ever seen, as well being as the most challenging to design and build.
Hugely useful again is Magnus Wenninger’s book Dual Models, published in 1989, though I suspect some of the drawings in it are less than fully accurate. That perhaps suggests no-one else has really tried making these shapes…it also testifies to how far out in front Wenninger was at the time.
Back then, Wenninger commented that few of these shapes had yet been studied or counted – let alone constructed – and although he suggested ‘computer analysis’ would be needed for further work it’s not clear that anyone’s actually done much of it in the intervening years. Surfing the web in 2012 I found George Hart and the Great Stella software had something to offer, but I’m left feeling that my models shown here may still be the first time someone’s really constructed them from scratch and put them on the web. I’ll be happy to be proved wrong, of course.
We start as usual with the baby of the group, the Triakis Tetrahedron, the dual of the Truncated Tetrahedron, both shown here. They both look at bit unexciting, but if you can imagine those twelve beige faces all extending and crashing into one another you might well believe it could get more interesting.
(By the way, in keeping with our usual practice for Duals we’ll stick to only one colour for each model, on the principle that we’re more interested in the vertices than the faces. You could argue against this since it’s the faces that we’re actually going to stellate, and it would be quite pretty to colour them individually: but since all the faces will meet up this means even the Tetrakis Tetrahedron will require twelve colours; and frankly my nerve fails for the more complex ones to come. For the moment, at least, we’ll rely on the lighting conditions to colour the different faces!)
Critical to working out the stellations is to map out, for any one face, where it meets all the others. In principle this is easy enough – you simply map it all out – but as we’ve said, for anything other than simple shapes like the Rhombic Dodecahedron or the simpler Archimedeans it’s a bit of a nightmare. I normally manage to do it, but it’s by far the most mentally stretching part of this whole job – and it usually only comes right as I build successive stellations. It’s very hard to do it all in advance without knowing roughly where you’re going!
But here, copied forward from later in the journey, is the stellation pattern based on one of those beige triangles:
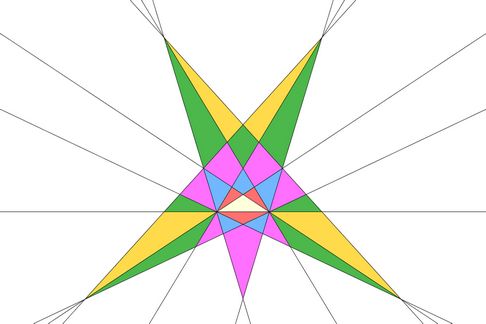
The first stellation extends the beige triangular faces out to their first meeting-points, and it should be easy to see how the red faces fit into the stellation pattern. Already the shape takes on a pleasing jewel-like look:
The second stellation follows by the usual process of extending the faces to meet up with each other, and they fill out the blue parts of the stellation diagram. Already, because the angles and shapes are all ‘funny’ this is a hideous job to calculate if you rely on trigonometry – so drawing out the stellation diagram with software like Geogebra is very useful in cutting straight to the geometry. Made up here in a nice shade of blue, we end up with a lovely gentle-looking crystal-ish shape:
The third stellation looks a bit ‘sharper’, a stunningly beautiful shape with 4 big spikes separated by 6 pairs of aggressive-looking crossed ‘fins’. Could I have known these were coming by looking at the second stellation and the stellation pattern? Well, yes, of course, and I thought ‘ooh, this is going to be good’ – but I was still bowled over when they finally emerged from my pink card, scissors and glue. It definitely looks like some evil alien deathcraft…
As usual there are lots of lines of symmetry and ‘cuttings’ to trace across the surface…
By way of reminder, here is the stellation pattern again. It should be easy to match these to the pink parts in the model:

So…are we finished? Well, no – there are two more yet, though the pink spike at the bottom marks the end of the road in its particular direction. The green and yellow areas in the pattern show there are two more stellations to come. (They also suggest by the time we get there I’ll need to buy a bigger display cabinet – even the pink one, as constructed, is about 30cm across!)
There’s another factor which makes things hugely more complicated. The proper definition of stellation (the one proposed by Miller and used particularly by Coxeter in his work on the Icosahedra) goes beyond the two-dimensional map I’ve shown here and counts all sorts of combinations of the solid ‘cells’ which lie between the planes. The solids I’ve developed here have been obtained by a simple process of ‘extension’, while the broader definition allows for all sorts of ‘taking away’ as well, and particularly for ‘chiral’ or ‘twisted’ forms which we’ll never find simply by working on an ‘extension’ process.
Analysing the combinations of all the possible cells is a truly complex piece of three-dimensional thought: Wenninger quotes B L Chilton in saying it produces no fewer than 138 just for the Tetrakis Tetrahedron, and for the more advanced Catalan solids the numbers increase rapidly into millions.
I haven’t seen a set of models that confirms even this one figure, either in cyberspace or in the real world – so there’s another grand project here. But for the moment I’ll be focussing on getting the green and yellow ones made.
With this we’ll call a halt to our exploration of Duals, but there are some Oddities that are well worth a look.









