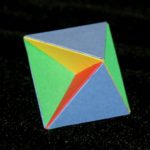
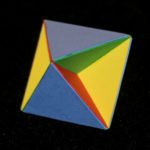
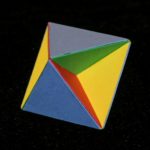
Blue triangles, red/yellow/green squares.
Logically the Tetrahemihexahedron is the first of the non-convex semi-regular polyhedra since it has the fewest faces (only 7 in fact – 4 triangles and 3 squares which cut through the centre), and the enclosing shape is just an Octahedron. The feel, and the symmetries, are those of a Tetrahedron, and that’s about as far as this one gets us – everything ahead of us is Cubic, Octahedral, Dodecahedral, Icosahedral etc. But it’s a cute little shape, and strangely I didn’t get round to making it until late in 2011.
Although it’s tiny, it has a couple of curious features. Firstly it’s a hemi-polyhedron, which means that some of its faces cut through the centre and we see both sides of them (and later on this means it’s dual is infinite); secondly it’s homomorphic with Steiner’s one-sided surface (here’s a link to the Wikipedia article on the Steiner Surface, though for once I think it manages to confuse rather than enlighten) which gives it sort-of Möbius strip properties. Thirdly, apart from pentagonal prisms and antiprisms it appears to be the only shape we can properly say has only seven faces, so as well as everything else it’s a Heptahedron.