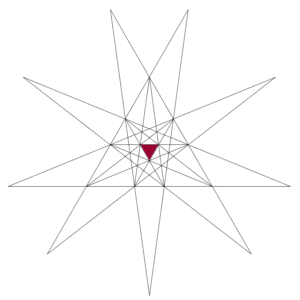
Having done the Dodecahedron, we obviously now must look at the stellations of the Icosahedron. This turns out to be a lot more complex: in fact there are 59 of these! To understand them, we have to consider the stellation diagram for the basic icosahedron:
This diagram shows the full pattern of intersections of just one triangular face of the icosahedron with the other faces. There are 20 faces in all, and if we exclude the red face itself and the one directly to the back of it. that still leaves 18 faces it has intersect with. So there are lots of lines, lots of cells, and lots of choices for making stellations. The truly expert write-ups are the books by Wenninger and Coxeter, but personally I’ve only ever made a few of these – and even then some of them have come from the wonderful model books by Tarquin. Here are my offerings…
Around Christmas 2011 I re-read Coxeter’s wonderful book, The 59 Icosahedra. Or rather, I managed to get just a few pages further into it than I’ve ever managed before.
The book inspired me so much that I resolved in the next year I would construct all the Stellations of the Icosahedron – meaning all of Coxeter’s 59. After all, Geogebra now makes drawing them up much easier, and a few experiments with white card and colour printing convinced me that I could, at long last, face the apparent come-down of building them with multi-coloured printed nets.
But it was clear that I couldn’t just launch into this – in particular, it’s all very well to use Geogebra to draw the nets and colour the polygons, but you have to know what colours to put where. Given that the task involves working with 10 colours in (probably) every possible combination, this is a huge challenge – and the only way I could think of was to build each model in turn, extending carefully out and considering each new one’s colours in the light of a very careful consideration of the previous model. And even speaking of ‘nets’ turns out to be a rather extravagant term – you’re lucky if you can lay out more than 10 elements into a net before you completely lose track of what colour goes where.
Other complications were things like having to find a set of 10 colours which would not only print out well and look different from each other, but would also look different when photographed – which is not as simple a question as you might think – and then managing the constant mental inversions required because some folds have to be scored on the outside, but others on the inside. And then I wanted the models to be coherently sized, so it would be obvious how the stellations followed on from each other. This sounds easy enough in principle, but if the final stellation were to fit into one of my cupboards this meant it had to be a maximum of about 32cm wide – which meant…ooh err, ratios of φ, φ2, φ3, φ4… the maximum length of the base icosahedron was 3cm. And many of the fiddly elements would be smaller!
After two weeks of faffing about, I had a base icosahedron, the 1st stellation, and two attempts at the 2nd stellation (the first attempt went a bit wobbly and is now used for experiments!) It felt as if I’d made a good start…but then things took a different turn. One night in London it occured to me to wonder… what else might be up for stellation? Why not the Truncated Cube? Or the other Archimedean solids? Well, presumably they’ve all been done; and presumably they would just collapse into the sequences we’ve already looked at…but no! The more I thought about it, the more interesting it all became – and though there are indeed similarities, it turns out no-one has written these things up, made the models or published them: no-one, at least, so far as I can find out. And so, through grey January and chilly February, I ploughed on – making ever more wonderful shapes. What follows is a statement of work-so-far; but it’s clear this could be another lifetime’s work… Stellations of the Truncated Tetrahedron