The set of 5 Platonics + 13 Archimedeans + 92 Johnsons + Prisms/Antiprisms has been proved to be the absolute limit of convex polyhedra that can be made with regular polygons. But when Johnson was compiling his list he found a number of near-misses: solids which look convincing when drawn on paper and constructed with cardboard, but which actually contain some very small inaccuracies which the eye doesn’t notice. These days the hunt is still on among a small tribe of polyhedronists (admittedly a very small tribe) and occasionally a new near-miss is claimed.
I’ve made the first one of these (an absolutely beautiful model even thought it’s a fake.) For the rest, I’ve copied the green pictures below from Craig Kaplan’s website at the University of Waterloo.
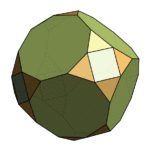
This one is obtained by inscribing an Enneagon (9 sides) on each face of an octahedron, then filling in the vertex holes with triangle-and-square caps. The triangles are not quite equilateral {1, 1, 1.05} but you’d never notice this unless you look it straight in the eye.
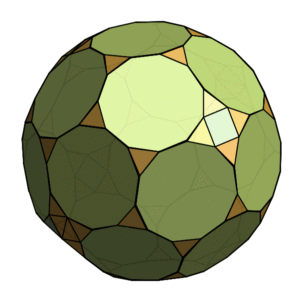An odd bizarre shape which appears to take a similar approach with 11-sided polygons and just a bit of snub-cube-ness thrown in. be a truncation of something (?) to produce 11-sided polygons (undecagons) connected by triangles, with a few extras thrown in to fill up the gaps. It has no mathematical validity at all, but it’s certainly curious.
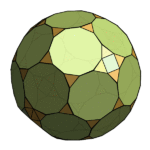
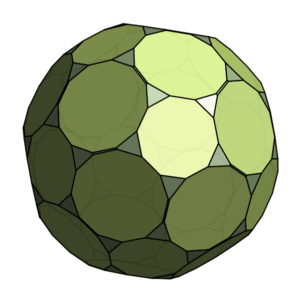An apparent Truncated Truncated Icosahedron, or Truncated Buckyball. In absolutely accurate terms this shape cannot exist – all those triangles and dodecagons would simply make the surface flat – but within practical margins of error it seems to work. The triangles’ sides turn out to be in the proportion 15:15:14, which really is too small an error to notice.
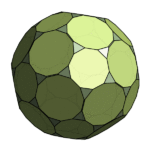
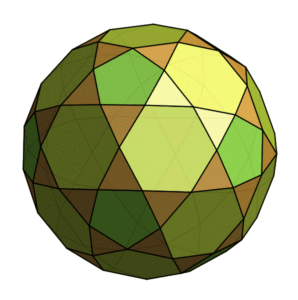This one looks like a more radical truncation of a Buckyball, a half-way house between two shapes in the same way the cuboctahedron and icosidodecahedron each sit between their two partner shapes. The partner shape to the Buckyball would of course be its dual – the Pentakis Dodecahedron – which is itself a surprisingly regular-looking shape, though in reality it isn’t regular at all. This suggests we might call the shape here the Trunco-icosi-pentakis-dodecahedron, but I’m not sure that would catch on.
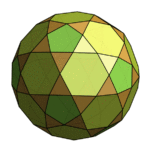
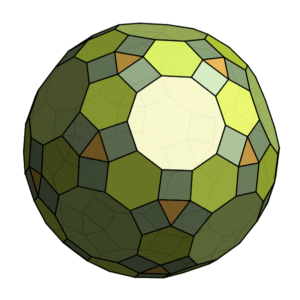Lastly in this section, what looks like an extension to the Great Rhombic Icosidodecahedron. Again it can’t possibly exist, because those hexagon-square-triangle vertices would simply be flat: my guess is that something about those hexagons isn’t quite right. But it’s quite a beauty.
This completes one strand of our basic journey through the Polyhedra, but there are at least three more strands – Compounds, Duality and Stellation – and then there are quite a lot of Oddities. Many of these are extremely beautiful, so please click on to Introduction to Compounds.